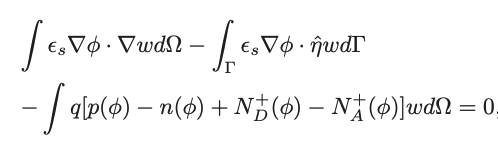Hi,
I am trying to implement a Non-Linear Poisson Solver for heterojunctions.
The weak formulation is given by
Here is my code and the error I am facing regarding the optimize function.
1 :
2 : load "msh3" (already loaded: msh3)
3 :
4 : // Base 2D mesh
5 : int n = 30; // Reduced for better conditioning
6 : real Lx = 10.0; // in whatever units you use
7 : real Ly = 5.0;
8 :
9 : mesh Th2D = square(n, n, [Lx * x, Ly * y]);
10 :
11 : // z boundaries of layers
12 : real[int] zlayers = [0, 4, 6, 10.0];
13 :
14 : int[int] r1 = [1, 1], rmid = [98, 98, 99, 99, 1, 56];
15 :
16 : int[int] ruplayer1 = [10, 11];
17 : int[int] ruplayer2 = [10, 11];
18 : int[int] ruplayer3 = [12, 13];
19 :
20 : int[int] rdownlayer1 = [14, 15];
21 : int[int] rdownlayer2 = [16, 17];
22 : int[int] rdownlayer3 = [16, 17];
23 :
24 : int[int] r2 = [2, 2];
25 : int[int] r3 = [3, 3];
26 :
27 : int MaxLayer = 20; // Reduced for better conditioning
28 :
29 : func zmin = 0;
30 : func zmax = 4;
31 :
32 : // Build each layer individually
33 : mesh3 Th1 = buildlayers(Th2D, MaxLayer, zbound=[zmin, zmax], region=r1, labelmid=rmid, labelup=ruplayer1, labeldown=rdownlayer1);
34 : mesh3 Th2 = buildlayers(Th2D, MaxLayer, zbound=[zlayers[1], zlayers[2]], region=r2, labelmid=rmid, labelup=ruplayer2, labeldown=rdownlayer2);
35 : mesh3 Th3 = buildlayers(Th2D, MaxLayer, zbound=[zlayers[2], zlayers[3]], region=r3, labelmid=rmid, labelup=ruplayer3, labeldown=rdownlayer3);
36 :
37 : // Merge them
38 : mesh3 Th3D = Th1 + Th2 + Th3;
39 :
40 : cout << “3D Mesh created with " << Th3D.nv << " vertices and " << Th3D.nt << " tetrahedra” << endl;
41 :
42 : // Define finite element space
43 : fespace Vh(Th3D, P1); // P1 finite elements (linear)
44 : Vh phi, w; // u is the solution, v is the test function
45 :
46 : real SiGeEg = 0.9; // SiGe bandgap [eV] - top and bottom regions
47 : real GeEg = 0.7; // Ge bandgap [eV] - center region
48 :
49 : // Physical constants and parameters (normalized units)
50 : real Nc = 1e17; // Reduced effective DOS [cm^-3]
51 : real q = 1.0; // Normalized electron charge
52 : real kbT = 0.0259; // thermal energy [eV]
53 : real Ef = 0.5; // Fermi level [eV] - moved to mid-gap
54 : real chii = 4.0; // electron affinity [eV]
55 : real phiref = 1.0; // reference potential [V] - set to 0 for simplicity
56 : real Eglocal = SiGeEg;
57 : real qval = 1.6e-19;
58 : real eps = 11.7;
59 :
60 :
61 : func real pphi(real phi){
62 : if (Th3D(x,y,z).region == 1 || Th3D(x,y,z).region == 3){
63 : Eglocal = SiGeEg;
64 : }
65 : else{
66 : Eglocal = GeEg;
67 : }
68 : real Ev = -(phi - phiref) - chii - Eglocal; // valence band edge
69 : real value1 = (Ev-Ef)/kbT;
70 :
71 : return Ncpow(value1,1.5)4/(3sqrt(pi)); // Clamp to avoid overflow
72 : }
73 :
74 : func real nphi(real phi){
75 : real Ec = -(phi - phiref) - chii; // conduction band edge
76 : real value2 = (Ef-Ec)/kbT;
77 : //return Ncexp((Ef - Ec) / kbT); // Clamp to avoid overflow
78 : return Nc * pow(value2,1.5) * 4/ (3*sqrt(pi));
79 : }
80 :
81 : real err = 1;
82 : real tol = 1e-6;
83 : real iter = 0;
84 : real maxIter = 10;
85 : real phiold = 2.7;
86 :
87 : while ((err > tol) && (iter < maxIter)) {
88 : iter = iter + 1;
89 :
90 : Vh Eglocal = (region==1 || region==3) ? SiGeEg : GeEg;
91 :
92 : Vh Ec = -(phiold - phiref) - chii; // Conduction band edge
93 : Vh Ev = -(phiold - phiref) - chii - Eglocal; // Valence band edge
94 :
95 : Vh xe = (Ef - Ec)/kbT;
96 : Vh xh = (Ev - Ef)/kbT;
97 :
98 : Vh nval = Nc * xe^3 * sqrt(xe) * 4.0 / (3.0 * sqrt(pi));
99 : Vh pval = Nc * xh^3 * sqrt(xh) * 4.0 / (3.0 * sqrt(pi));
100 :
101 : Vh rho = q * (pval - nval);
102 :
103 : varf a(phi, w) =
104 : int3d(Th3D)( eps * (dx(phi)*dx(w) + dy(phi)*dy(w) + dz(phi)*dz(w)) )
105 : + int3d(Th3D)( rho * w )
106 : + on(14, phi=0.0)
107 : + on(12, phi=1.0);
108 :
109 : matrix A = a(Vh, Vh);
110 : real[int] b = a(0, Vh);
111 :
112 : set(A, solver=sparsesolver);
113 : phi = A^-1 * b;
114 :
115 : err = sqrt(int3d(Th3D)((phi - phiold)^2));
116 : cout << "Iter " << iter << " Error = " << err << endl;
117 : phiold = phi;
118 : }
119 :
120 : sizestack + 1024 =8112 ( 7088 )
– Square mesh : nb vertices =961 , nb triangles = 1800 , nb boundary edges 120 rmdup= 0
3D Mesh created with 58621 vertices and 324000 tetrahedra
– FESpace: Nb of Nodes 58621 Nb of DoF 58621
nan != nan diff nan => Sorry error in Optimization (q) add: int2d(Th,optimize=0)(…)
remark if you add (.. , optimize=2) then you remove this check (be careful);
current line = 110
Exec error : In Optimized version
– number :1
Exec error : In Optimized version
– number :1
err code 8 , mpirank 0