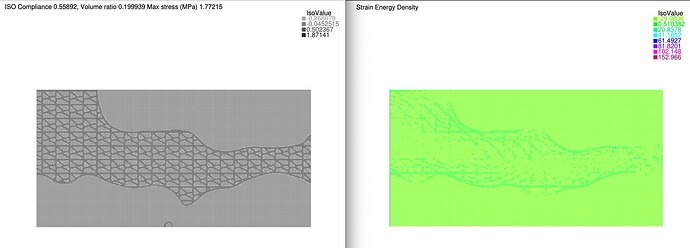
I’m a beginner and currently having trouble with analysis results.
Strain energy density is not supposed to be negative, correct?
However, the analysis using the code below gives negative values for it.
Chat GPT and gemini pointed out a mistake in this part problem elasticity(u1,u2,v1,v2)=int2d(Thh)(mu*(2.0*dx(u1)*dx(v1)+2.0*dy(u2)*dy(v2)+dy(u1)*dx(v2)+dx(u2)*dy(v1)+dy(u1)*dy(v1)+dx(u2)*dx(v2))+lambda*(dx(u1)+dy(u2))*(dx(v1)+dy(v2)))-int1d(Thh,3)(f1*v1+f2*v2)+on(1,u1=0,u2=0);.
If anyone has any idea, I’d really appreciate any help or advice.
load "iovtk"
load "medit"
load "gmsh"
real startTime = clock();
// define small unit cell length
real Lsl=0.1; // L of small lattice
real Hsl=0.1; // H of small lattice
// define small lattice
real isl=20; //the square root of number of small lattice; must a integer
real jsl=10; //the square root of number of small lattice; must a integer
// define the whole domain size:
real L = Lsl*isl, H = Hsl*jsl;
real ksl,xx1,yy1,xx2,yy2,xsl,ysl;
// define gray for plot
real[int] gray = [ 0, 0 , 1.0, 0.0, 0 , 0 ]; //Plot < HSV (Hue, Saturatiovn, Value) >
// Domain dimensions
real x0 = 0, x1 = L;
real y0 = 0.0, y3 = H;
real y1 = H * (2.0 / 5.0);
real y2 = H * (3.0 / 5.0);
// Build mesh to plot
int xmeshnum=250; //200;
int ymeshnum=xmeshnum*H/L;
mesh Thplot=square(xmeshnum,ymeshnum,[x0+(x1-x0)*x,y0+(y3-y0)*y],flags=2);
int[int] l1=[2, 2, 0, 1] ;
int[int] l2=[0, 3, 0, 1] ;
int[int] l3=[0, 2, 2, 1] ;
mesh Th0 = readmesh("Th0_rand.msh");
mesh Th1=square(xmeshnum,ymeshnum*2/5,[x0+(x1-x0)*x,y0+(y1-y0)*y],label=l1,flags=1); // bottom
mesh Th2=square(xmeshnum,ymeshnum/5,[x0+(x1-x0)*x,y1+(y2-y1)*y],label=l2,flags=1); // middle: traction
mesh Th3=square(xmeshnum,ymeshnum*2/5,[x0+(x1-x0)*x,y2+(y3-y2)*y],label=l3,flags=1); // upper
mesh Thh = Th1+Th2+Th3;
fespace Vh2(Th0,P2);
Vh2 oldphi,phi,vphi,Xi=0.0;
fespace Vh1(Thh,P2);
Vh1 iflc,Xisl,Xisurface,if1,Xilc,Xislall=0.0,ifabov,ifbelo;
fespace Vh00(Th0,P1);
Vh00 oldphi0; //!!oldphi must use P1!!
//Read phi from phi.sol
oldphi0[]=readsol("phi.sol");oldphi=oldphi0;
fespace Vh3(Thplot,P2);
Vh3 vplot, Xiplotsurface,Xiplotallsmlattice, Xiplotfinal, Xiplotstress, Xiplotdensity;
fespace Vh4(Thh,[P1,P1]);
Vh4 [u1,u2],[v1,v2];
fespace Vh5(Thh,P2);
Vh5 xphi,xvphi,xoldphi,Xitemp;
// Make macro smoother
real dt = 0.1; // pseudo time interval
real tau = 2e-5; // Diffusion Coefficient [from 0.0 to 2e-2]
int ci=0;
problem RDE(phi,vphi) = int2d(Th0)(phi*vphi)-int2d(Th0)(oldphi*vphi) + int2d(Th0)( dt*tau*(dx(phi)*dx(vphi)+dy(phi)*dy(vphi)) ) + on(3,phi=1.0);
RDE;
real philo=0.01;
real phihi=0.99;
real vratio;
real rerror=1;
real alpha=0.4;
ci=0;
while (rerror>0.001){
ci=ci+1;
if (ci>50) break;
Xi=phi>(0.5*philo+0.5*phihi);
Xi=min(Xi,1);
Xi=max(Xi,0);
vratio=int2d(Th0)(Xi)/int2d(Th0)(1.0);
rerror=abs(vratio-alpha)/alpha;
//cout << vratio << endl;
if (vratio<alpha){
phihi=0.5*philo+0.5*phihi;
}
else{
philo=0.5*philo+0.5*phihi;
}
}
//( -------- make boundary width more uniform (*wsl adjusted)---------
Vh2 dphix = dx(phi);
Vh2 dphiy = dy(phi);
// Compute normalized gradient magnitude
Vh2 gradNorm = sqrt(dphix^2 + dphiy^2) + 1e-8; // Avoid division by zero
real wsl=0.005; // Cui: adjusted due to adding gradNorm
Xisurface=0.5*(1-sign(abs(phi-philo)-wsl * gradNorm));
// --------- make boundary width more uniform (*wsl adjusted)---------)
//real wsl=0.18; // proportional to the width of macro surface
// Xisurface=0.5*(1-sign(abs(phi-philo)-wsl));
Xiplotsurface=Xisurface;
// Voronoi method to create small unit cell
mesh Thsm=square(50,50,[0.0+(Lsl-0.0)*x,0.0+(Hsl-0.0)*y],flags=2); // small unit cell
// inside unit cell
fespace Vhsm(Thsm,P1);
Vhsm Xism;
savesol("x.sol",Thsm,x,order=1);
savesol("y.sol",Thsm,y,order=1);
// Voronoi
exec("python3 voro_sample.py 0.03973992579376708,0.05468867517001769,0.0383462292074418,0.0239366029134648,0.027641785408882735,0.02517881684907429,0.042190540447518673,0.043540666250316926 iso_voro True");
Xism[]=readsol("Xism.sol");
for (int i = 0; i < isl; ++i){
for (int j = 0; j < jsl; ++j){
real xperiod=i*Lsl;
real yperiod=j*Hsl;
// zero if outside small lattice cell
iflc=((Lsl+xperiod-x)*(x-0-xperiod)>-0.1*L/xmeshnum)*((Hsl+yperiod-y)*(y-0-yperiod)>-0.1*L/xmeshnum);
mesh Thsmmove = movemesh(Thsm, [x+xperiod, y+yperiod]);
fespace Vhsmmove(Thsmmove,P1);
Vhsmmove Xismmove;
Xismmove = Xism(x-xperiod,y-yperiod);
Xislall=Xislall+Xismmove*iflc;
}
}
Xiplotallsmlattice=Xislall;
// Overlap -> inside macro
Xislall=Xi*Xislall;
//Add macro BC
Xislall=Xislall+Xisurface;
Xislall=min(1.0,Xislall);
Xislall=max(0.0,Xislall);
//no smoothing, otherwise too round
// make sure the same voluem ratio
xoldphi=Xislall;
problem RDE2(xphi,xvphi) = int2d(Thh)(xphi*xvphi)-int2d(Thh)(xoldphi*xvphi) + int2d(Thh)( dt*tau*(dx(xphi)*dx(xvphi)+dy(xphi)*dy(xvphi)) ) + on(3,xphi=1.0);
RDE2;
real xphilo=0.01;
real xphihi=2.0;
rerror=1;
alpha=0.2;
ci=0;
while (rerror>0.001){
ci=ci+1;
if (ci>50) break;
//Xitemp=xphi>(0.5*xphilo+0.5*xphihi);
Xitemp=0.5*(1+tanh(50*(xphi-(0.5*xphilo+0.5*xphihi))));
vratio=int2d(Thh)(Xitemp)/int2d(Thh)(1.0);
rerror=abs(vratio-alpha)/alpha;
//cout << vratio << endl;
if (vratio<alpha){
xphihi=0.5*xphilo+0.5*xphihi;
}
else{
xphilo=0.5*xphilo+0.5*xphihi;
}
}
Xislall=Xitemp;
cout << "ci = " << " " << ci << endl;
// Define stress analysis
real E0 = 10000000000.0; // Young's Modulus
real Emin = 10000000.0;
real nu = 0.33; //poisson's ratio
Xislall=min(1.0,Xislall);
Xislall=max(0.0,Xislall);
func E = max(E0*Xislall^4,Emin); // Elastic modulus
func lambda = E*nu*(1.0/((1.0+nu)*(1.0-nu))); // Lame constant for plane stress
func mu = E*(1.0/(2.0*(1.0+nu))); // Lame constant
real f = 10000.0;
real f1 = f * cos(-0.5*pi);
real f2 = f * sin(-0.5*pi);
problem elasticity(u1,u2,v1,v2)=int2d(Thh)(mu*(2.0*dx(u1)*dx(v1)+2.0*dy(u2)*dy(v2)+dy(u1)*dx(v2)+dx(u2)*dy(v1)+dy(u1)*dy(v1)+dx(u2)*dx(v2))+lambda*(dx(u1)+dy(u2))*(dx(v1)+dy(v2)))-int1d(Thh,3)(f1*v1+f2*v2)+on(1,u1=0,u2=0);
elasticity;
// find max of von mises stress
func e11 = dx(u1);
func e22 = dy(u2);
func e12 = (dy(u1)+dx(u2))/2.0;
func sigma11 = 2*mu*e11+lambda*(e11+e22);
func sigma22 = 2*mu*e22+lambda*(e11+e22);
func sigma12 = 2*mu*e12;
func sigmavm = sqrt(sigma11^2+sigma22^2-sigma11*sigma22+3*sigma12^2);
fespace Vh6(Thh,P1);
Vh6 svm;
svm = sigmavm;
real maxsigma = svm[].max/1e6;
//plot all lattice + shape + shell
Xiplotfinal=Xislall;
real compliance = int1d(Thh,3)(f1*u1+f2*u2);
real ratio = int2d(Thh)(Xislall)/int2d(Thh)(1.0);
real endTime = clock();
string caption=" ISO Compliance "+ compliance + ", Volume ratio " + ratio+" Max stress (MPa) " + maxsigma;
func strainEnergyDensity = 0.5 * (sigma11 * e11 + sigma22 * e22 + 2.0 * sigma12 * e12);
Vh6 sed;
sed = strainEnergyDensity;
Xiplotdensity = sed;
plot(Xiplotfinal, nbiso=4,fill=1,hsv=gray, cmm=caption,value=true,WindowIndex=2,ps="plot_final.eps");
plot(Xiplotdensity, fill=1, value=true, nbiso=8, cmm="Strain Energy Density", WindowIndex=4, ps="plot_strain_energy_density.eps");
cout << "compliance,cost,stress" << endl;
cout << compliance << "@" << endTime - startTime << "@" << maxsigma << endl;