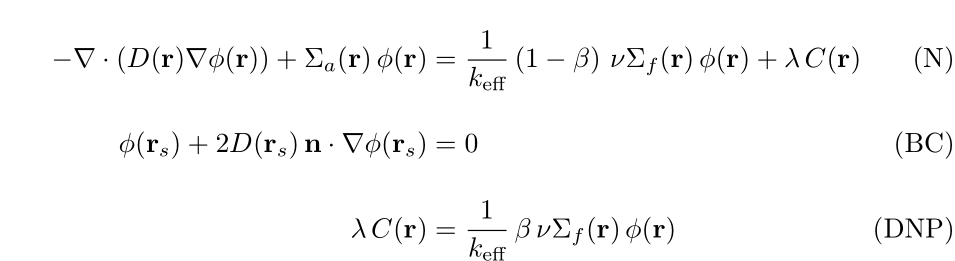EigenValue, vectors and block matrices

General Discussion
1

I’m solving a simple 2D neutron diffusion problem, with delayed neutron precursors (DNPs). In steady-state, the equations look like this:

problem_neutro
problem_neutro955×261 8.63 KB

We see clearly that, since we’re in steady-state, we could plug (DNP) into (N) and obtain a standalone neutron diffusion equation.
So I tested 3 ways of solving this problem:

  1. The simplest way, which is to plug (DNP) into (N) and solve for \phi only;
  2. Assembling a single big matrix, for (N) and (DNP) at the same time;
  3. Building block matrices and then assembling big matrices.

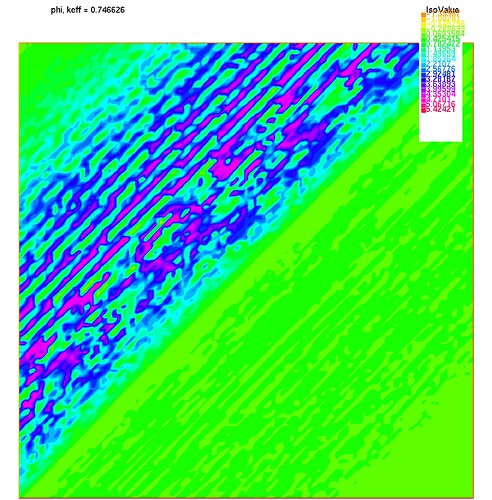
All three of these methods give the same eigenvalue keff, but only 1. and 2. give the (correct) eigenvector \phi, while 3. gives a very different output:

neutro_1
neutro_11902×1941 339 KB

neutro_2
neutro_21889×1935 339 KB

neutro_3
neutro_31885×1915 329 KB

In the future, I think method 3. is the way to go for more complicated problems, so I’d like to get it working. Maybe I should manipulate the eigenvectors differently?

Here are the three scripts.
neutro_1.edp (1.6 KB)
neutro_2.edp (2.2 KB)
neutro_3.edp (2.5 KB)

2

Dear Ruggero,
With the block matrix definition, the ordering of the dofs is not the same as in the
product space definition fespace PHICh(Th, [P2, P2]);
In the latter the dof are interlaced, whereas in the block matrix the dofs are listed one block after the other.
Therefore you have to do some reordering in order to have the right interpretation.

fespace PHIh(Th, P2);
fespace Ch(Th, P2);
PHIh bphi;
Ch bc;
for (int nn=0;nn<nev;++nn) {
 [bphi[],bc[]]=eVphi[nn][];
 [eVphi[nn],eVc[nn]]=[bphi,bc];
}

full code
neutro_3.edp (2.7 KB)

3

Dear François,

Super, got it! Thanks a lot :smiley:

Ruggero