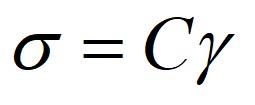Hello, Professor, I used the following one-dimensional periodic boundary code, but something went wrong,
load “msh3”
border OX(t=-40,40){x=t;y=0;}
int m=100; // grid points on x-interval [0,1]
real h=1./m;
meshL Th=segment(m);real T=1;
real k=0.3;
real x0=4;
real A=12k^2;
real omega=4k^2;
real dt=0.01;fespace Uh(Th,P1,periodic=[[1, x]]);//periodic boundary condition
Yes because in 1d the syntaxe is show in example
Hello, according to your reply, I used the linear element P1. There is no problem with the program. However, using the quadratic element P2, I found that this item
-int1d(Thf)(dxx(u1)*dx(v))
will lead to program interruption. Why？
60 : sizestack + 1024 =4460 ( 3436 )
– Build Nodes/DF on mesh : n.v. 321, n. elmt. 320, n b. elmt. 2
nb of Nodes 640 nb of DoF 640 DFon=1100
– FESpace: Nb of Nodes 640 Nb of DoF 640
– Build Nodes/DF on mesh : n.v. 641, n. elmt. 640, n b. elmt. 2
nb of Nodes 1280 nb of DoF 1280 DFon=1100
– FESpace: Nb of Nodes 1280 Nb of DoF 1280
current line = 37
Assertion fail : (0)
line :245, in file …/femlib/P012_3dCurve.cpp
Assertion fail : (0)
line :245, in file …/femlib/P012_3dCurve.cpp
err code 6 , mpirank 0
Hello, I use the following command
fespace Uh(Th,P3,periodic=[[1],[2]]);
. My periodic boundary condition is
，
problem KDV(u1,v)=int1d(Thf)(u1v/dt)-int1d(Thf)(u0v/dt)-int1d(Thf)(dxx(u1)dx(v))
+int1d(Thf)(u0dx(u1)*v);
So is this command right?
You use a old version do freefem++ with the computation of dxx in 1d is not computed
Need version 4.11 (the last to day).
Thank you very much for your reply. 
Hello Prof. Hecht,
I have a doubt if FreeFEM can work on 1D periodic multiphysics problem where the physical quantities are coupled. For example, I’m now working on 1d piezoelectric composites with two phases: fiber and matrix. The displacement and electric potential are coupled by the following equation
I use the following code to solve the governing differential equation
load "msh3"
real L0 = 1.;
meshL Th = segment(100,[L0*x]);
fespace Vh(Th,P1,periodic=[[1],[2]]);
real cf = 0.5;
real C1 = 131, e1 = 10.99, k1 = 2.081; // fiber
real C2 = 145.5, e2 = 17.36, k2 = 15.1; // matrix
func Cp = C1*(x<cf*L0) + C2*(x>=cf*L0 && x<=L0);
func ep = e1*(x<cf*L0) + e2*(x>=cf*L0 && x<=L0);
func kp = k1*(x<cf*L0) + k2*(x>=cf*L0 && x<=L0);
Vh N1u,M1u,N1us,v1,v2,xx;
xx = x;
problem microflucNMu([N1u,M1u], [v1,v2]) = int1d(Th)( (Cp*dx(N1u)+ep*dx(M1u))*dx(v1) +
(ep*dx(N1u)-kp*dx(M1u))*dx(v2) ) +
int1d(Th)( Cp*dx(v1)+ep*dx(v2) );
microflucNMu;
plot([xx[],N1u[]],cmm = "distribution of N1u");
plot([xx[],M1u[]],cmm = "distribution of M1u",WindowIndex=1);
However, the solution I got for N1u and M1u are not periodic! Meanwhile, if I degrade to uncoupled elasticity problem using the following equation and code
problem microflucNus(N1us,v1) = int1d(Th)( Cp*dx(N1us)*dx(v1) ) +
int1d(Th)( Cp*dx(v1) );
microflucNus;
plot([xx[],N1us[]],cmm = "distribution of N1us",WindowIndex=2);
Then, I can get the periodic solution for N1us.
I don’t know where the problem is for my multiphysics code. I’ve attached my code below. I used FreeFEM v4.11.
Periodic-1D.edp (1.1 KB)
Thanks a lot if you or anyone else can help.
Hello, about 1D periodic boundary command, my periodic boundary conditions need to be met
U (a) =u (b) and dx (U (a)) =dx (U (b)), use this command
fespace Uh(Th,P3,periodic=[[1],[2]]);
Where periodic=[[1], [2]] represents U (a) =u (b), but how to satisfy the periodic boundary condition dx (U (a)) =dx (U (b)) of the first derivative?
Remark, if the function is periodic when all derivative are periodic.
Thank you for your reply. In fact, does this command
fespace Uh(Th,P3,periodic=[[1],[2]]);
mean that the original function and its derivatives of all orders satisfy the characteristics of periodic functions in finite element space?
yes, this is a math propriety!